
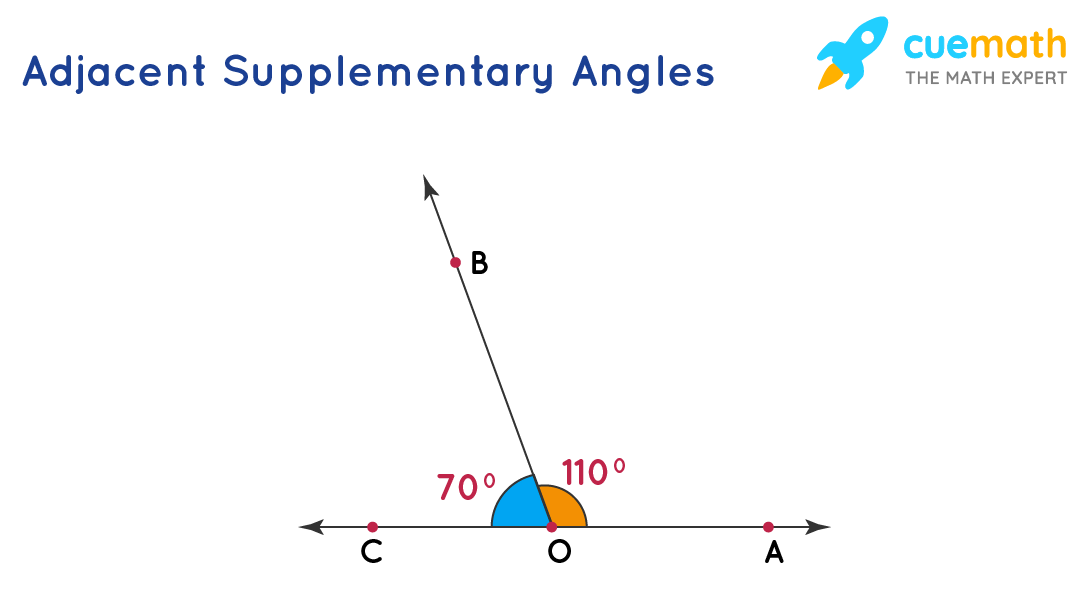
This one doesn’t look like an angle at all:īut in fact, it’s called a full angle. This is a useful thing to know because we’ll need it to understand linear pairs later on.īut before we get to that, let’s look at the other oddball. When it’s drawn like this, we can see that ∠ABC does exist and has a measure of 180 degrees. It looks like a straight line, and it has a measure of 180 degrees. Those are the three main types of angles as determined by measure, but there are two more oddballs we need to know about. Obtuse angles also have to be less than 180 degrees. In this case, angle ABC has a measure of 140 degrees, which is greater than 90. If we make an angle so that it has a measure that is greater than 90 degrees, we create an obtuse angle, which looks like this: Our original angle would be part of an acute triangle, since it measures 45 degrees, which is less than 90: When an angle has a measure that is smaller than 90 degrees, it’s called an acute triangle. We most often see right angles in squares, rectangles, and right triangles, but they can appear in other places too. Whenever we see an angle with that square we know it is exactly 90 degrees. Notice that it has a different angle symbol than our first angle. Let’s look at a variation of our two-ray angle, but this time let’s make it so that they are perpendicular to each other, which means the angle between them is 90 degrees: The measure of an angle is important in classifying angles, as we’re about to see. If we wrote this out, we would write it like this: If we were to place one on our trusty angle we would find that it measures 45 degrees: Speaking of measuring, remember the protractor? We use it to measure angles. Sometimes you’ll see lowercase letters instead of numbers or Greek symbols like \(\theta\) or \(\alpha\). But most of the time we like to use letters to name our angles, since the numbers could be confused with the measure of an angle. Since most of us have three names, it’s only fair that angles have a bunch too. We can now call it ∠1 or we can call it ∠ABC or we can call it ∠B. Now we have an additional name for this angle. Sometimes angles will be labeled with numbers inside the arc, like this: So it’s important to be precise when dealing with more than one angle. In this case, we’d have to call the angles by their long names, because point B is the vertex of ∠ABC, ∠DBC, and ∠DBA! If we asked someone to just look at ∠B they wouldn’t know which of these we meant. Be careful though, because sometimes a single point can be the vertex of multiple angles, like this: In this case, we could also call this angle B. If the point that is the vertex is only a part of one angle then we can use a shorter name.
We can actually call this ∠CBA and it is just as correct. Here, B is the vertex so the B goes between the A and the C. When naming angles with three letters, the vertex point must be in the middle. Now we can refer to our angle as angle ABC (∠ABC).

Here’s our simple angle again but with a few points added on the rays: Sometimes we have many angles, so in order to tell them apart, we have a system for naming them. We usually see vertices whenever lines meet or in polygons like triangles and quadrilaterals. We’ve also created a vertex, which is the point where the two rays meet. If we take this ray and add another ray to it that has the same endpoint, we’ve created an angle. A ray is a line with a single endpoint that extends infinitely in one direction. The rays corresponding to supplementary angles intersect the unit circles in points having the same $y$-coordinate, so the two angles have the same sine (and opposite cosines).Hi, and welcome to this video about angles If you define the sine by means of the unit circle, then this image should explain the fact: Let's stick to right triangles, which allow to define the sine for acute angles: if $\alpha=\widehat=\alpha'$, that is, $\alpha'=\pi-\alpha$, then It depends a lot on how you define the sine.


 0 kommentar(er)
0 kommentar(er)
